فروش پروژه تشخيص اثر انگشت با شبكه عصبی و فازی با نرم افزار MATLAB
كد: 526
عنوان پروژه: فروش پروژه تشخيص اثر انگشت با شبكه عصبی و فازی با نرم افزار MATLAB
قالب بندی: m
دسته: كامپيوتر – MATLAB
قيمت: 40.000 تومان
قابليت اجرا در نرم افزار: MATLAB
شرح مختصر:
فروش پروژه تشخيص اثر انگشت با شبكه عصبی و فازی با نرم افزار MATLAB
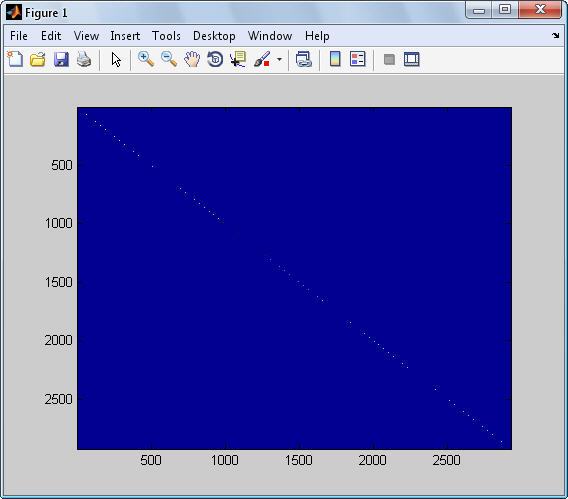
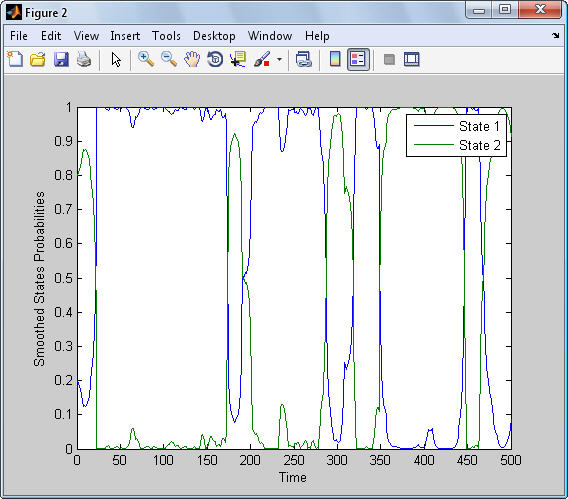
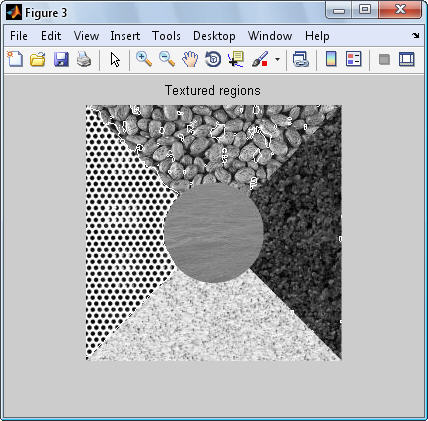
عكس خروجی برنامه
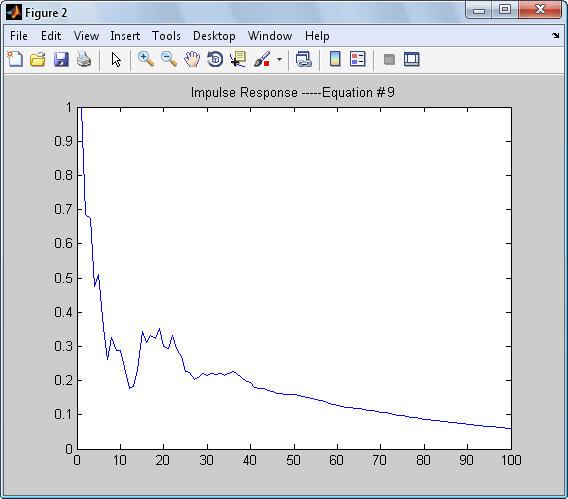
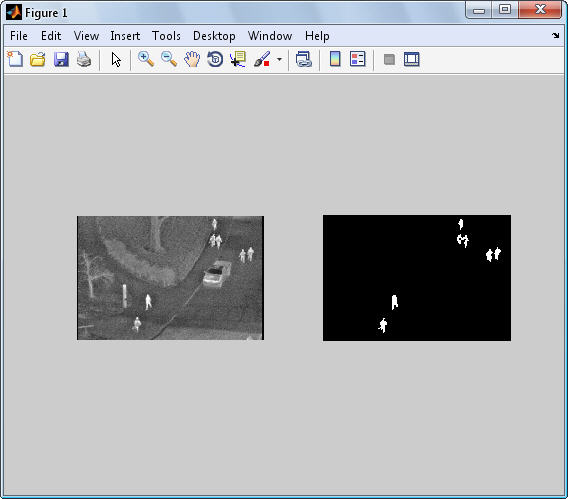
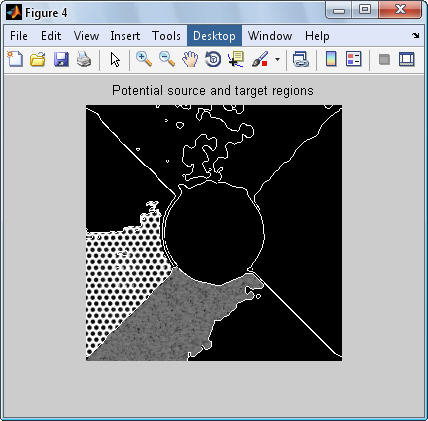
عكس 2
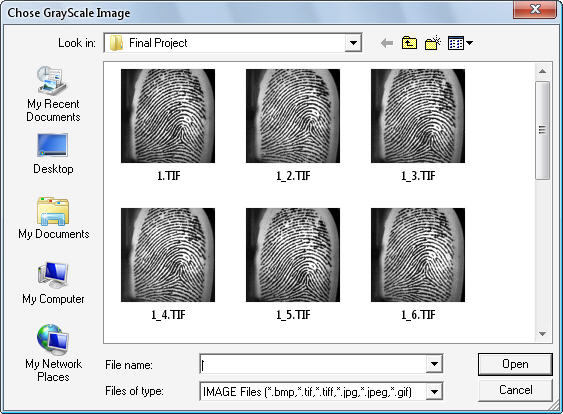
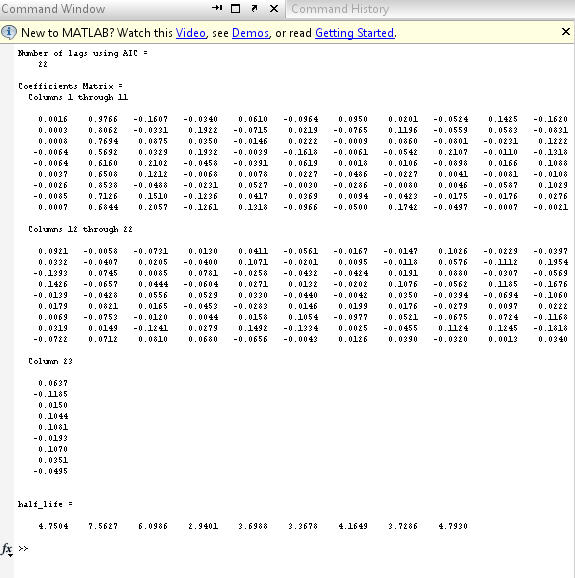
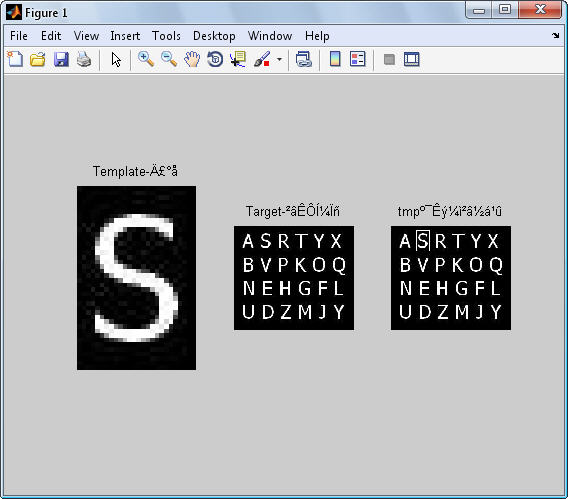
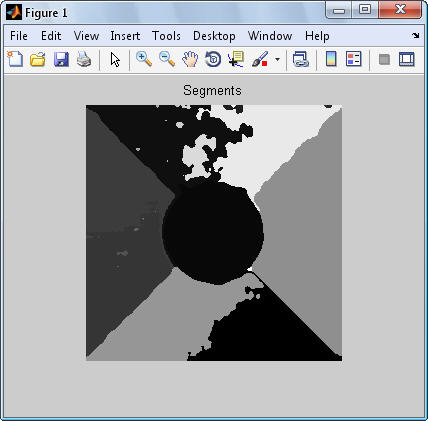
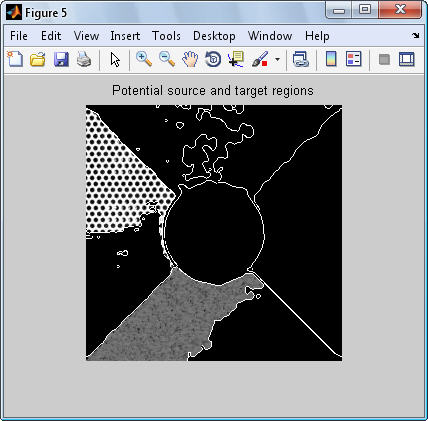
عكس 4
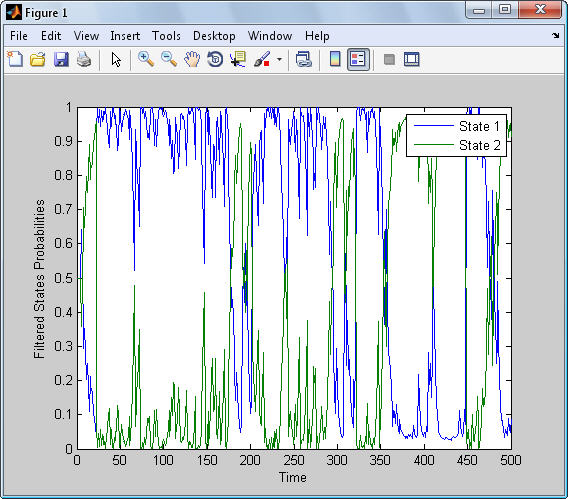
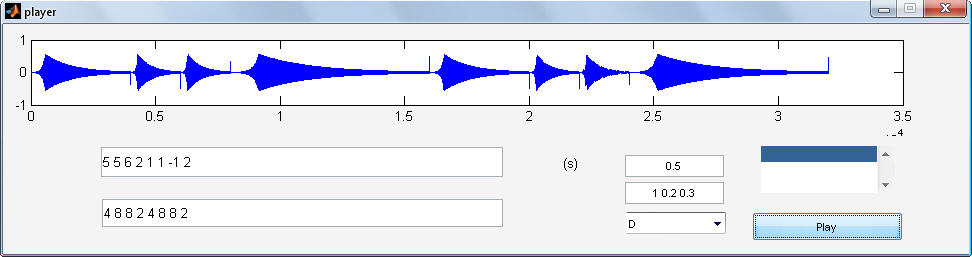
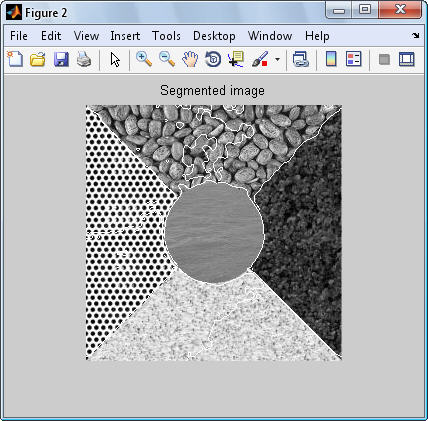
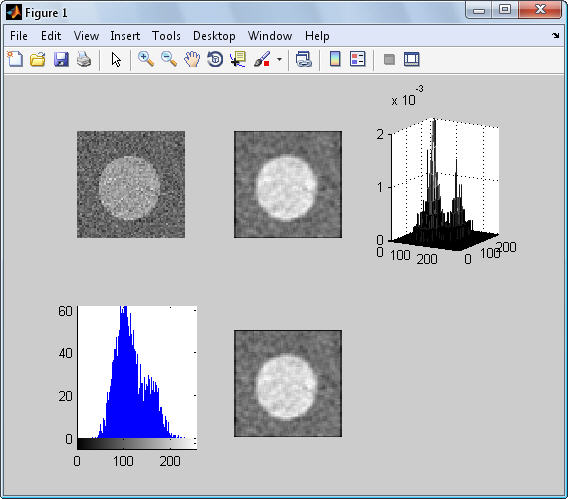
عكس 5
عكس 6
برای خريد اين پروژه با شماره 09360703858
يا آدرس ايميل nn4e@aol.com در تماس باشيد.